

The ACT® WorkKeys Test Applied Mathematics Free Practice Test
The ACT® WorkKeys applied mathematics test is one of the 8 sections of the ACT WorkKeys test, an assessment tool that evaluates work-related skills and job performance. This section measures your mathematical reasoning, problem-solving ability, and critical thinking.
Passing the applied mathematics section of the test is essential for receiving the National Career Readiness Certificate (NCRC).
The following page will give you the information and practice needed to ace the ACT WorkKeys applied mathematics test, with sample questions, detailed answers, and preparation tips.
Scoring high on the WorkKeys test will demand a strong grip at several mathematics levels, requiring proper practice and guidance. Make sure to check our:

David, ACT WorkKeys Expert at JobTestPrep
Have a question? Contact me at:
ask_the_team@jobtestprep.com
The ACT WorkKeys applied math test assesses numerical reasoning and problem-solving techniques required in the workplace. As such, the questions are based on real-life scenarios that employees experience daily.
The test has 5 difficulty levels, ranging from 3 to 7. The levels are built on top of one another, each incorporating the skills assessed in the previous level. Thus, in level 6, you will need the skills from levels 4 and 5.
You will have 55 minutes to answer 34 questions.
You are allowed to use a calculator and the ACT WorkKeys formula sheet.
This section of the WorkKeys test can be administered by computer or pencil-and-paper, depending on the testing center you registered at.
If you're looking for free practice, you can check our Free Workkeys Practice Test.
In level 3 of the WorkKeys applied math test, you will be presented with word problems that need to be translated into math equations. You will be given all the information you need in a logical order, and you will need to demonstrate numerical skills such as converting fractions and converting between decimals and percentages.
Let's see how it looks –
Three elephants drank 250 gallons of water in two days. Elephant A drank the same amount of water each day. On the second day, Elephant B drank three gallons less than on the first day, and elephant C drank three gallons more than on the first day. How many gallons did the elephants drink on the second day?
A. 119 B. 125 C. 131 D. 250In order to figure out how many gallons the elephants drank on the second day, first sum up the information:
| Elephant A | Elephant B | Elephant C |
|---|---|---|
| A | B | C |
| A | B-3 | C+3 |
Add the gallons each drank on the two days:

The elephants drank 250 gallons in two days; accordingly:

Note that the three extra gallons that elephant C drank on the second day cancel out the three fewer gallons Elephant B drank on the second day. Thus, together, the three elephants drank the same amount of water on the first day as on the second. If you have keen enough mathematical intuition, you may have noticed this without having to use any equations at all, but if you did use math - don't worry, this is how those instincts are developed.
If you chose answers (A) or (C), review the given information and check for differences. If you chose answer (D), you may have calculated the total amount of water the elephants drank on those two days.
The correct answer is B
A college fraternity planned a three-day study marathon. On the first day, they studied 75% of the time, ate for 3 hours, and slept the rest of the time. On the second day, they studied 50% of the time, ate for 4 hours, and slept the rest of the time. On the third day, they slept 1⁄3 of the time. How many hours in total did the fraternity members sleep during the three days?
Note that one day contains 24 hours.
A. 15 hours B. 19 hours C. 24 hours D. 38 hoursCalculate the number of hours the fraternity slept every day:
Start by converting the percentages into absolute hours.
First day (24 hours):
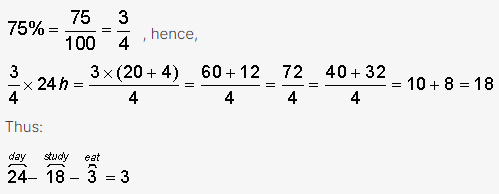
The students slept for 3 hours on the first day.

Total number of hours spent in sleep: 3+8+8 = 19
The correct answer is B
In addition to the type of questions you answered in level 3, you will be presented with questions in which the information can be out of order or include extra and unnecessary information and questions, which can include graphs. You will need to demonstrate numerical skills such as evaluating ratios, rates, and proportions, and calculating averages of a set of numbers.
Let's check it out –
Dan took a two-hour walk around a round lake. The radius of the lake is 6 feet. What was Dan's average speed?
A. 2π feet\hour B. 6π feet/hour C. 12π feet/her D. 24π feet/houtAny time we need to calculate the speed, we should use the formula time x speed = distance:
The time is given. Now, in order to calculate the speed, first find the distance.
The lake is round with a radius of 6 feet. Accordingly, if Dan took a walk around the lake, the distance he walked is also the perimeter of the lake.
Therefore, use the formula of a circle’s perimeter in order to calculate the perimeter of the lake:

Therefore, Dan's average speed is 6π.
If you chose any other answer, review the solution and your calculations.
The correct answer is B
The ingredients for a barrel of moisturizer are: 7⁄8 of a gallon glycerin, 1⁄4 of a gallon alcohol, 3⁄4 of a gallon fruit oil, and 4⁄32 of a gallon fragrance. In the perfume shop, the workers divided 7 barrels into 70 bottles. After a week, 52 bottles remained unsold. From the remaining bottles, the workers created 70 cream jars.
What is the moisturizer volume of one jar of cream?
A. 1⁄7 of a gallon B. 52⁄350 of a gallon C. 1⁄5 of a gallon D. 14⁄52 of a gallonCalculate the volume of one barrel by using 32 as a common denominator:

The volume of a single barrel is, therefore, 2 gallons.
Next, calculate the amount of moisturizer in each jar according to the given information.

A jar contains 52⁄350 of a gallon.
If you chose answer (D), review your calculations. If you chose answers (A) or (C), review your calculations of the transition process from a barrel to a jar.
The correct answer is B
In addition to the type of questions you answered in levels 3 and 4, you will be presented with questions that may require several calculations and logical steps. You will need to demonstrate numerical skills such as adding and subtracting fractions with different denominators and calculating percentages.
Let's view practice questions –
There are 25 monkeys in the zoo. The average weight of 5 of those monkeys is 100 pounds, and the average weight of the rest of them is 75 pounds. What is the average weight of all the monkeys in the zoo in pounds?
A. 80 lb B. 85 lb C. 87.5 lb D. 91 lbFirst, summarize the given information:
5 monkeys 🠖 100 lb per monkey, on average.
25-5 = 20 monkeys 🠖 75 lb per monkey, on average.
In order to find the average weight of all the monkeys in the zoo, calculate the total weight of all the monkeys:

Next, in order to calculate the average, substitute the total weight in the formula:

The average weight of all the monkeys in the zoo is 80 lb.
If you chose any other answer, check your calculations.
The correct answer is A
A pencil is sketched using a rectangle and an isosceles triangle. The length of the pencil is 12 inches. The length of the rectangular section is five times longer than its width, and the height of the triangle is 2 inches. What is the perimeter of the pencil?

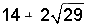
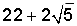
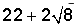
In order to solve this problem, calculate the length of all outer sides of both the rectangle and the triangle.
From the given information, it is known that the total length of the pencil is 12 inches, and the height of the triangle is 2 inches; therefore, the length of one side of the rectangle is: 12-2 = 10 inches.
Given that one side of the rectangle is five times longer than the other:
And, since opposite sides of a rectangle have the same length (or “congruent”):

In an isosceles triangle, the height is perpendicular to the base and divides the base into two equal parts, thus the sides of the triangle can be calculated using the Pythagorean Theorem:

The perimeter of the pencil is:
![]()
If you chose answer (A), you probably confused the base and the other sides of the triangle. If you chose answer (C), you probably forgot to divide the base by two, and if you chose answer (D), review the solution.
The correct answer is B
In addition to the type of questions you answered in levels 3 to 5, you will be presented with questions that may require translation from verbal to mathematical expression and multiple-step calculations. You will need to demonstrate numerical skills such as calculating reverse percentages and converting units within and between systems of measurement.
Let's solve some practice questions –
Boston Fall is a new self-service salad restaurant. Dan went to the restaurant and asked for half a cucumber, one large potato, two carrots, three onions, three tomatoes, and one corncob.
The cost of one cucumber is a dollar; one large potato is 1⁄2 a dollar; one carrot is 3⁄4 of a dollar; one onion is 1⁄8 of a dollar; one tomato is 2 1⁄3 dollars; and one corncob is 3⁄8 of a dollar.
Dan came back with two friends: Michael asked for the same ingredients in his salad but with half the amount of each vegetable, and Brian asked for the same ingredients but with triple the amount of each vegetable. Dan offered to pay for everything.
What is the difference between the price Dan paid for the three salads and the price Dan would have paid for his salad only?